ГДЗ Алгебра 7 клас Істер - Розв'язання вправи № 1073

Розв'язання до підручника «Алгебра» для 7 класу.
Автор: О.С. Істер.
Умова вправи № 1073
Побудуйте в одній системі координат графіки функцій $y = 1,5x - 4$ і $y = 2$ та знайдіть координати точки їх перетину.
Розв'язок вправи № 1073
Коротке рішення
1) Знайдемо дві точки для графіка $y = 1,5x - 4$:
- $x = 0 \implies y = 1,5 \cdot 0 - 4 = -4 \rightarrow (0; -4)$
- $x = 4 \implies y = 1,5 \cdot 4 - 4 = 6 - 4 = 2 \rightarrow (4; 2)$
2) Графіком $y = 2$ є горизонтальна пряма, що проходить через точку $(0; 2).$
3) Побудуємо графіки в одній системі координат:
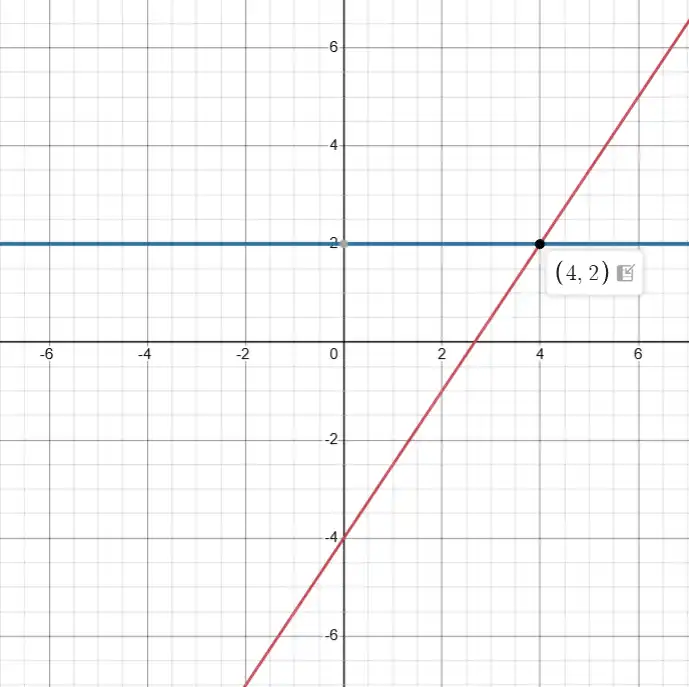
4) За графіком точка перетину має координати $(4; 2).$
Відповідь: $(4; 2).$
Детальне рішення
Ключ до розв'язання: Щоб знайти точку перетину, нам потрібно точно побудувати обидва графіки функцій. Точка, де вони зустрічаються, має координати, які одночасно задовольняють обидві формули. Це практичне застосування знань про те, як працює лінійна функція.
- Як будувати $y = 1,5x - 4$: Ми обираємо зручні числа для ікса. Якщо взяти $x=0,$ ми одразу знаходимо точку на вертикальній осі ($-4$). Якщо взяти $x=4,$ результат буде $2.$ Через ці дві точки проводимо пряму.
- Як будувати $y = 2$: Це стала функція. Її графік — це рівна лінія "на висоті" $2$ над віссю іксів. Вона показує, що ігрек завжди дорівнює двійці, незалежно від ікса.
- Пошук перетину: На малюнку ми бачимо, що похила лінія "дотягнулася" до висоти $2$ саме тоді, коли ми відійшли від центру вправо на $4$ клітинки. Отже, координати точки $(4; 2).$



















Коментування доступне тільки зареєстрованим
Будь ласка, увійдіть через Google, щоб залишити коментар.