ГДЗ Алгебра 7 клас Істер - Розв'язання вправи № 1175

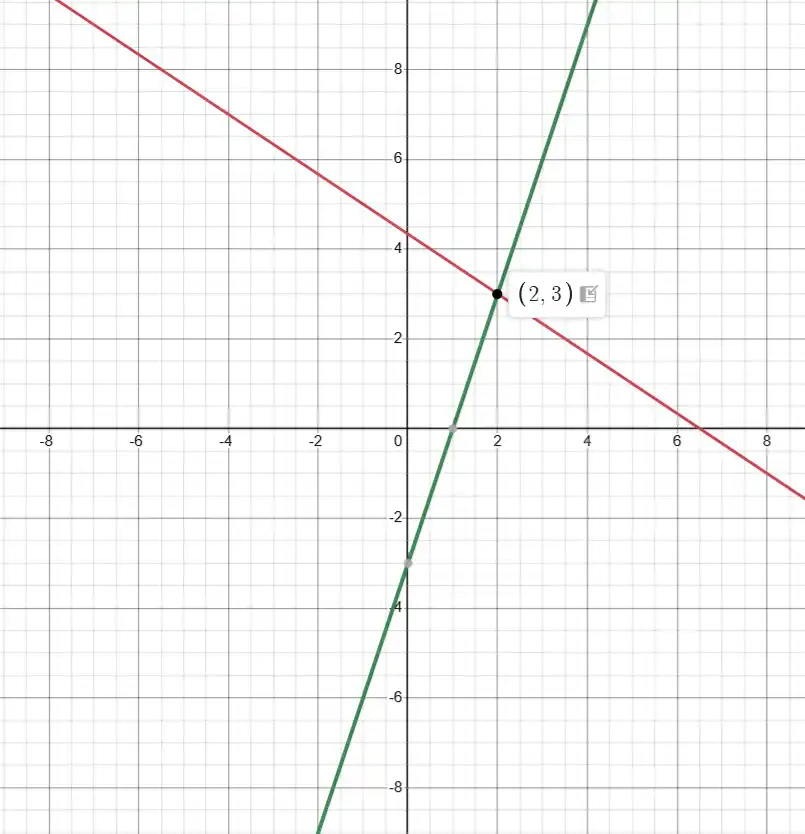
1) Для системи $\begin{cases} 2x + 3y = 13, \\ 3x - y = 3 \end{cases}$ знайдемо точки:

Перша пряма: $y = \frac{13 - 2x}{3}.$ Точки: $(2; 3)$ та $(5; 1).$

Друга пряма: $y = 3x - 3.$ Точки: $(1; 0)$ та $(2; 3).$

Точка перетину: $(2; 3).$

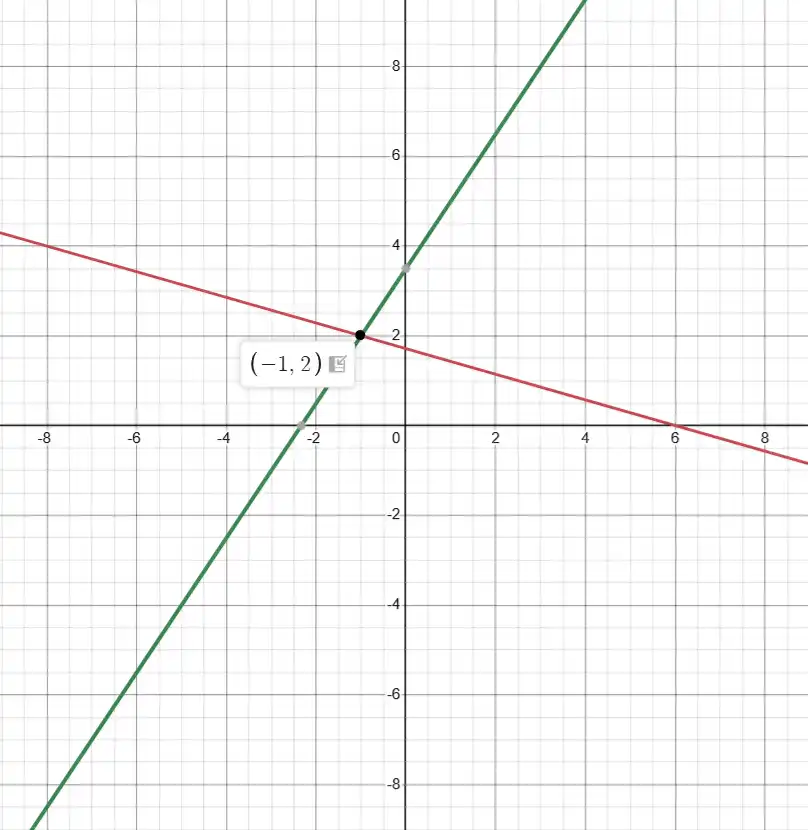
2) Для системи $\begin{cases} 2x + 7y = 12, \\ 3x - 2y = -7 \end{cases}$ знайдемо точки:

Перша пряма: $y = \frac{12 - 2x}{7}.$ Точки: $(-1; 2)$ та $(6; 0).$

Друга пряма: $y = 1,5x + 3,5.$ Точки: $(-1; 2)$ та $(1; 5).$

Точка перетину: $(-1; 2).$

Відповідь: 1) $(2; 3);$ 2) $(-1; 2).$

Для успішного розв'язання ми спершу виражаємо змінну $y$ через $x$ в кожному рівнянні. Це дозволяє нам легко підібрати координати двох точок для побудови кожної прямої. В першому пункті точка перетину $(2; 3)$ знайдена аналітично підбором зручних значень $x$. В другому пункті важливо було підібрати такі значення $x$, щоб чисельник дробу $\frac{12 - 2x}{7}$ ділився на 7 без остачі. Точність побудови на координатній площині дозволяє підтвердити, що знайдені пари чисел задовольняють обидва рівняння системи одночасно.